Греки (Greeks) —
количественные характеристики чувствительности цены (премии) производного инструмента (например, [url=http://calvera.ru/forum/viewtopic.php?f=33&t=135]опциона[/url]) к изменению тех или иных величин, оказывающих влияние на стоимость производного инструмента или портфеля финансовых инструментов.
Название "греки" происходит от греческого алфавита, буквами которого принято обозначать некоторые из этих коэффициентов.
Использование греков
Греки являются жизненно важными инструментами в области управления рисками. Каждый грек показывает чувствительность стоимости портфеля к небольшому изменению лежащего в его основе параметра (цены базового актива, времени до экспирации, волатильности, безрисковой процентной ставки и т.п.), так что компоненты риска могут быть рассмотрены по отдельности для достижения требуемой степени сбалансированности портфеля.
Греки в
модели Блэка-Шоулза довольно легко вычислить, что позволяет трейдерам существенно снизить влияние неблагоприятных изменений конъюнктуры рынка на портфели производных финансовых инструментов.
Наиболее распространенные из греков — это производные первого порядка: Delta (Дельта), Vega (Вега), Theta (Тета) и Rho (Ро), а также Gamma (Гамма) — производная второго порядка цены опциона. Остальные коэффициенты чувствительности используются реже, и их перечень довольно обширен.
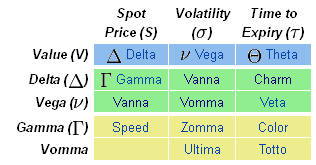
- options_table.png (7.42 KiB) Viewed 39873 times
[spoiler="Греки первого порядка"]
Греки первого порядка
Delta
Delta
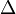
- delta.png (200 Bytes) Viewed 39874 times
показывает отношение скорости изменения цены опциона к скорости изменения цены базового актива. Delta является первой производной цены
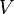
- V.png (220 Bytes) Viewed 39874 times
опциона по отношению к цене базового актива
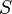
- S.png (226 Bytes) Viewed 39874 times
.
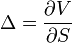
- delta_f1.png (565 Bytes) Viewed 39874 times
У стандартных (
ванильных) опционов Delta принимает значения от 0 до 1 для купленных call-опционов (или проданных put-опционов), и от -1 до 0 для купленных put-опционов (или проданных call-опционов). Чем глубже купленный call-опцион в деньгах (ITM), тем динамика его цены точнее повторяет динамику цены базового актива (Delta стремится к 1); чем дальше опцион от денег (OTM), тем меньше он реагирует на изменение цены базового актива (Delta стремится к нулю).
Дельта портфеля, в который входят инструменты с общим базовым активом, равна сумме соответствующих дельт каждого инструмента, входящего в портфель. Поскольку дельта базового актива всегда равна 1, трейдер может дельта-хеджировать свою позицию базовым активом, покупая или продавая его в количестве, необходимом для нейтрализации суммарной дельты портфеля. Такой портфель будет сохранять свою стоимость независимо от изменений цены базового актива (данное утверждение справедливо только для небольших движений цены базового актива и на коротком промежутке времени, при этом не учитываются возможные изменения других рыночных условий, таких как волатильность и ставка доходности для безрисковых инвестиций).
Абсолютное значение дельты опциона близко, но не равно, вероятности того, что опцион истечёт в деньгах (ITM). По этой причине некоторые опционные трейдеры используют дельту для приблизительной оценки вероятности такого события. Например, если дельта опциона вне денег (OTM) равна 0,15, то вероятность выхода этого опциона в деньги и экспирации там приблизительно составляет 15%. Опционы около денег (ATM) имеют дельту около 0,5, что примерно соответствует 50% вероятности того, что они будут в деньгах на момент экспирации. Для более точного расчёта вероятности экспирации опциона в деньгах используется Dual Delta, которая является первой производной цены опциона по страйку.
Для двух европейских опционов call и put с общим базовым активом, ценой исполнения (страйком), датой экспирации и без дивидендных выплат, сумма абсолютных значений их дельт равна 1, другими словами, дельта call-опциона (положительна) минус дельта put-опциона (отрицательна) равно 1.
Vega
Vega отражает чувствительность к изменению волатильности. Вега является производной цены опциона по отношению к волатильности базового актива.
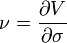
- vega_f1.png (524 Bytes) Viewed 39874 times
Для обозначения веги используется греческая буква ню (
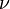
- nu.png (190 Bytes) Viewed 39874 times
). Учёные иногда обозначают вегу буквой каппа (
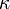
- kappa.png (192 Bytes) Viewed 39874 times
), а также буквой тау (
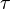
- tau.png (168 Bytes) Viewed 39874 times
), но значительно реже.
Вега обычно отражает количество денег, на которое увеличится (или уменьшится) стоимость опциона при увеличении (или снижении) волатильности базового актива на 1%. Если вега отрицательна, то стоимость опциона падает с ростом волатильности и растёт при снижении волатильности.
Theta
Theta
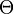
- theta.png (227 Bytes) Viewed 39874 times
отражает изменение стоимости опциона с течением времени, то есть величину временного распада.
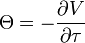
- theta_f1.png (621 Bytes) Viewed 39874 times
Математический результат, полученный по приведенной выше формуле, даёт значение в расчёте на год. Как правило, этот результат делят на количество дней в году, чтобы получить сумму денег, на которую снижается цена опциона за один день. Тета почти всегда отрицательна для купленных опционов и положительна для проданных. Исключением может являться европейский put-опцион, находящийся глубоко в деньгах (ITM). Величина теты для портфеля может быть определена как сумма тет для каждой отдельной позиции, входящей в портфель.
Стоимость опциона можно разделить на две части: внутреннюю стоимость и временн
ую стоимость. Внутренняя представляет собой сумму денег, которую можно было бы получить, если исполнить опцион немедленно. То есть у call-опциона со страйком $50 при цене базового актива $60 внутренняя стоимость равна $10, при этом put-опцион того же страйка будет иметь нулевую внутреннюю стоимость. Оставшаяся часть цены опциона приходится на временную стоимость. Чем больше времени до экспирации, тем выше временная стоимость опциона (при прочих равных условиях) и медленнее временной распад. С приближением даты экспирации временной распад ускоряется (тета увеличивается по модулю), а временная стоимость уменьшается вплоть до нуля.
Rho
Rho
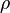
- rho.png (205 Bytes) Viewed 39874 times
является мерой чувствительности к величине безрисковой процентной ставки. Rho — это производная стоимости опциона по отношению к безрисковой процентной ставке.
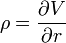
- rho_f1.png (564 Bytes) Viewed 39874 times
Rho обычно выражается в виде суммы денег, на которую увеличится (или уменьшится) цена опциона при повышении (или снижении) безрисковой процентной ставки на 1,0% годовых (100 базисных пунктов).
За исключением чрезвычайных обстоятельств, стоимость опциона менее чувствительна к изменениям безрисковой процентной ставки, чем к изменениям других параметров. По этой причине ро является наименее часто используемым греком первого порядка.
Lambda
Lambda
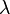
- lambda.png (199 Bytes) Viewed 39874 times
, Omega
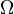
- omega.png (226 Bytes) Viewed 39874 times
или упругость — величина, показывающая на сколько процентов изменится цена опциона при изменении цены базового актива на 1%. Её также называют рычагом, плечом, передачей.
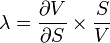
- lambda_f1.png (812 Bytes) Viewed 39874 times
Например, если цена опциона равна $5, дельта 0,2 и цена базового актива $100, то Lambda = 0,2 * $100/$5 = 4, то есть при увеличении цены базового актива на 1% ($1 от $100) цена опциона увеличится на 4% ($0,2).
[/spoiler]
[spoiler="Греки второго порядка"]
Греки второго порядка
Gamma
Gamma
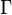
- gamma.png (173 Bytes) Viewed 39874 times
показывает отношение скорости изменения дельты опциона к скорости изменения цены базового актива. Гамма является второй производной цены
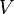
- V.png (220 Bytes) Viewed 39874 times
опциона по отношению к цене базового актива
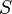
- S.png (226 Bytes) Viewed 39874 times
. Все купленные опционы имеют положительную гамму, все проданные — отрицательную. Наибольшее абсолютное значение гаммы имеют опционы около денег (ATM), которое постепенно уменьшается когда опцион становится в деньгах (ITM) или вне денег (OTM).
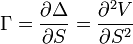
- gamma_f1.png (879 Bytes) Viewed 39874 times
Когда трейдер стремится создать эффективный дельта-хеджированный портфель, он может также нейтрализовать гамму портфеля, что будет гарантировать эффективное хеджирование в более широком диапазоне ценовых движений базового актива. Однако, при нейтрализации гаммы портфеля, снижается коэффициент
альфа.
Vanna
Vanna, также известная как DdeltaDvol и DvegaDspot, является производной второго порядка от цены опциона по отношению к цене базового актива и волатильности. Математически она эквивалентна DdeltaDvol (первой производной дельты по волатильности), которая показывает чувствительность дельты опциона к изменению волатильности; или DvegaDspot (первой производной веги по цене базового актива), оценивающей изменение чувствительности опциона к изменению волатильности при движении цены базового актива. Vanna может быть полезна для контроля чувствительности дельта- или вега-хеджированного портфеля к изменению, соответственно, волатильности или цены базового актива.
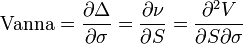
- vanna_f1.png (1.3 KiB) Viewed 39871 times
Vomma
Vomma, Volga, выпуклость веги, гамма веги или dTau/dVol — величина, отражающая чувствительность второго порядка к волатильности. Vomma является второй производной стоимости опциона по волатильности, или, другими словами, vomma измеряет скорость изменения веги при изменении волатильности. При положительной vomma, позиция становится более длинной по веге при увеличении подразумеваемой волатильности, и более короткой по веге при снижении IV.
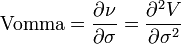
- vomma_f1.png (1008 Bytes) Viewed 39871 times
Charm
Charm или распад дельты отражает мгновенную скорость изменения дельты с течением времени. Charm также называют DdeltaDtime (первая производная дельты по времени). Charm является производной второго порядка от стоимости опциона по отношению к цене базового актива и времени. Это также производная теты по отношению к цене базового актива. Charm помогает поддерживать эффективный дельта-хедж, особенно при переносе позиции через выходные и праздники.
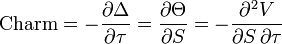
- charm_f1.png (1.39 KiB) Viewed 39871 times
Математический результат, полученный по вышеуказанной формуле, даёт значение в расчёте на год. Часто бывает полезно разделить его на количество дней в году, чтобы получить величину распада дельты за сутки. Такая оценка является достаточно точной, если количество дней до экспирации опциона относительно велико. При приближении даты экспирации charm может меняться довольно быстро, что заметно искажает суточную оценку распада дельты.
Veta
Veta или DvegaDtime показывает скорость изменения веги с течением времени, или скорость распада веги. Veta — вторая производная цены опциона: по волатильности и по времени.
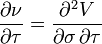
- veta_f1.png (794 Bytes) Viewed 39871 times
Обычной практикой является деление результата, полученного по вышеуказанной формуле, на количество дней в году и на 100, чтобы получить процентное изменение веги за один день.
Vera
Vera (иногда Rhova) показывает скорость изменения Rho при изменении волатильности. Вера является второй производной цены опциона: по волатильности и по безрисковой процентной ставке. Vera может быть использована для оценки воздействия изменения волатильности на Rho-хеджирование.
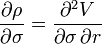
- vera_f1.png (796 Bytes) Viewed 39871 times
[/spoiler]
[spoiler="Греки третьего порядка"]
Греки третьего порядка
Color
Color, распад гаммы или DgammaDtime показывает скорость изменения гаммы с течением времени. Color — производная третьего порядка цены опциона: дважды по цене базового актива и один раз по времени. Color может быть полезен для прогнозирования изменения гамма-хеджа с течением времени.
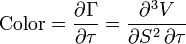
- color_f1.png (1.07 KiB) Viewed 39866 times
Математический результат, полученный по вышеуказанной формуле, даёт значение в расчёте на год. Часто бывает полезно разделить его на количество дней в году, чтобы получить величину распада гаммы за сутки. Такая оценка является достаточно точной, если количество дней до экспирации опциона относительно велико. При приближении даты экспирации color может меняться довольно быстро, что заметно искажает суточную оценку распада гаммы.
Speed
Speed показывает скорость изменения гаммы при изменении цены базового актива. Эту величину иногда называют гаммой гаммы или DgammaDspot. Speed — третья производная цены
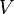
- V.png (220 Bytes) Viewed 39874 times
опциона по отношению к цене базового актива
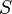
- S.png (226 Bytes) Viewed 39874 times
. Speed может быть полезна при мониторинге дельта- или гамма-хеджа портфеля.
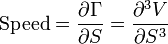
- speed_f1.png (1.02 KiB) Viewed 39866 times
Ultima
Ultima или DvommaDvol показывает чувствительность vomma к изменению волатильности. Ultima — третья производная стоимости опциона по волатильности.
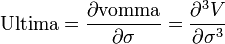
- ultima_f1.png (1.15 KiB) Viewed 39866 times
Zomma
Zomma или DgammaDvol показывает скорость изменения гаммы при изменении волатильности. Zomma — третья производная стоимости опциона: дважды по цене базового актива и один раз по волатильности. Zomma может быть полезна для мониторинга гамма-хеджа портфеля, и поможет трейдеру предвидеть изменения в эффективности хеджирования при изменении волатильности.
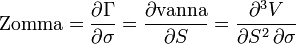
- zomma_f1.png (1.46 KiB) Viewed 39866 times
[/spoiler]
[spoiler="Формулы расчёта опционных греков"]
Формулы расчёта греков
Греки стандартных (
ванильных) опционов в рамках
модели Блэка-Шоулза для заданной цены базового актива
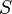
- S.png (226 Bytes) Viewed 39874 times
, цены исполнения опциона (страйке)
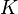
- K.png (245 Bytes) Viewed 39865 times
, безрисковой процентной ставке

- r.png (175 Bytes) Viewed 39865 times
, годовой дивидендной доходности
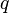
- q.png (206 Bytes) Viewed 39865 times
, времени до экспирации
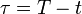
- tau_f1.png (359 Bytes) Viewed 39864 times
и волатильности
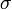
- sigma.png (196 Bytes) Viewed 39864 times
рассчитываются следующим образом:
| Call-опционы | Put-опционы |
|---|
| Цена опциона |
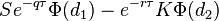 - Цена call-опциона
- price_call.png (969 Bytes) Viewed 39864 times
|
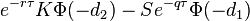 - Цена put-опциона
- price_put.png (1023 Bytes) Viewed 39864 times
|
|---|
|
|---|
| Delta |
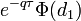 - Delta call-опциона
- delta_call.png (560 Bytes) Viewed 39864 times
|
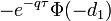 - Delta put-опциона
- delta_put.png (594 Bytes) Viewed 39864 times
|
|---|
| Vega |
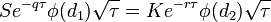 - Vega опциона
- vega_call_put.png (1.05 KiB) Viewed 39864 times
|
|---|
| Theta |
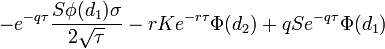 - Theta call-опциона
- theta_call.png (1.76 KiB) Viewed 39862 times
|
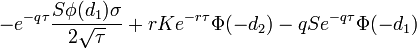 - Theta put-опциона
- theta_put.png (1.9 KiB) Viewed 39862 times
|
|---|
| Rho |
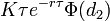 - Rho call-опциона
- rho_call.png (674 Bytes) Viewed 39862 times
|
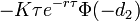 - Rho put-опциона
- rho_put.png (724 Bytes) Viewed 39862 times
|
|---|
|
|---|
| Gamma |
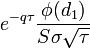 - Gamma опциона
- gamma_call_put.png (844 Bytes) Viewed 39861 times
|
|---|
| Vanna |
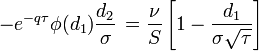 - Vanna опциона
- vanna_call_put.png (1.38 KiB) Viewed 39861 times
|
|---|
| Charm |
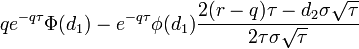 - Charm call-опциона
- charm_call.png (1.81 KiB) Viewed 39861 times
|
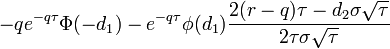 - Charm put-опциона
- charm_put.png (1.73 KiB) Viewed 39861 times
|
|---|
|
|---|
| Speed |
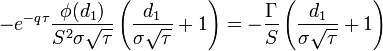 - Speed опциона
- speed_call_put.png (2.28 KiB) Viewed 39861 times
|
|---|
| Zomma |
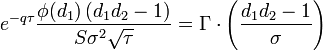 - Zomma опциона
- zomma_call_put.png (1.75 KiB) Viewed 39861 times
|
|---|
| Color |
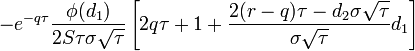 - Color опциона
- color_call_put.png (2.18 KiB) Viewed 39861 times
|
|---|
|
|---|
| Veta |
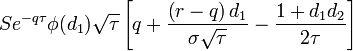 - Veta опциона
- veta_call_put.png (1.8 KiB) Viewed 39860 times
|
|---|
| Vomma |
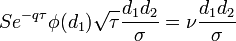 - Vomma опциона
- vomma_call_put.png (1.26 KiB) Viewed 39860 times
|
|---|
| Ultima |
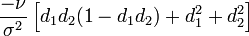 - Ultima опциона
- ultima_call_put.png (1.12 KiB) Viewed 39860 times
|
|---|
|
|---|
| Dual Delta |
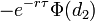 - Dual Delta call-опциона
- dualdelta_call.png (566 Bytes) Viewed 39860 times
|
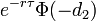 - Dual Delta put-опциона
- dualdelta_put.png (571 Bytes) Viewed 39860 times
|
|---|
| Dual Gamma |
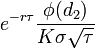 - Dual Gamma опциона
- dualgamma_call_put.png (856 Bytes) Viewed 39860 times
|
|---|
где
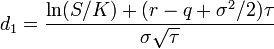
- d1.png (1.45 KiB) Viewed 39860 times
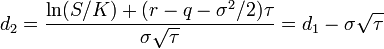
- d2.png (1.66 KiB) Viewed 39860 times
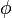
- phi_small.png (225 Bytes) Viewed 39864 times
— функция стандартной нормальной плотности вероятности
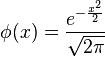
- phi_small_f1.png (828 Bytes) Viewed 39860 times
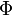
- phi_big.png (202 Bytes) Viewed 39864 times
— функция стандартного нормального распределения
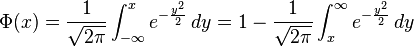
- phi_big_f1.png (1.83 KiB) Viewed 39860 times
[/spoiler]
[term]Греки (Greeks) -- количественные характеристики чувствительности цены (премии) производного инструмента (например, [url=http://calvera.ru/forum/viewtopic.php?f=33&t=135]опциона[/url]) к изменению тех или иных величин, оказывающих влияние на стоимость производного инструмента или портфеля финансовых инструментов.[/term]
Название "греки" происходит от греческого алфавита, буквами которого принято обозначать некоторые из этих коэффициентов.
[b]Использование греков[/b]
Греки являются жизненно важными инструментами в области управления рисками. Каждый грек показывает чувствительность стоимости портфеля к небольшому изменению лежащего в его основе параметра (цены базового актива, времени до экспирации, волатильности, безрисковой процентной ставки и т.п.), так что компоненты риска могут быть рассмотрены по отдельности для достижения требуемой степени сбалансированности портфеля.
Греки в [url=http://calvera.ru/forum/viewtopic.php?f=33&t=224]модели Блэка-Шоулза[/url] довольно легко вычислить, что позволяет трейдерам существенно снизить влияние неблагоприятных изменений конъюнктуры рынка на портфели производных финансовых инструментов.
Наиболее распространенные из греков — это производные первого порядка: Delta (Дельта), Vega (Вега), Theta (Тета) и Rho (Ро), а также Gamma (Гамма) — производная второго порядка цены опциона. Остальные коэффициенты чувствительности используются реже, и их перечень довольно обширен.
[attachment=42]options_table.png[/attachment]
[spoiler="Греки первого порядка"]
[size=120][b]Греки первого порядка[/b][/size]
[b]Delta[/b]
Delta [attachment=57]delta.png[/attachment] показывает отношение скорости изменения цены опциона к скорости изменения цены базового актива. Delta является первой производной цены [attachment=59]V.png[/attachment] опциона по отношению к цене базового актива [attachment=58]S.png[/attachment].
[attachment=56]delta_f1.png[/attachment]
У стандартных ([url=http://calvera.ru/forum/viewtopic.php?f=33&t=225]ванильных[/url]) опционов Delta принимает значения от 0 до 1 для купленных call-опционов (или проданных put-опционов), и от -1 до 0 для купленных put-опционов (или проданных call-опционов). Чем глубже купленный call-опцион в деньгах (ITM), тем динамика его цены точнее повторяет динамику цены базового актива (Delta стремится к 1); чем дальше опцион от денег (OTM), тем меньше он реагирует на изменение цены базового актива (Delta стремится к нулю).
Дельта портфеля, в который входят инструменты с общим базовым активом, равна сумме соответствующих дельт каждого инструмента, входящего в портфель. Поскольку дельта базового актива всегда равна 1, трейдер может дельта-хеджировать свою позицию базовым активом, покупая или продавая его в количестве, необходимом для нейтрализации суммарной дельты портфеля. Такой портфель будет сохранять свою стоимость независимо от изменений цены базового актива (данное утверждение справедливо только для небольших движений цены базового актива и на коротком промежутке времени, при этом не учитываются возможные изменения других рыночных условий, таких как волатильность и ставка доходности для безрисковых инвестиций).
Абсолютное значение дельты опциона близко, но не равно, вероятности того, что опцион истечёт в деньгах (ITM). По этой причине некоторые опционные трейдеры используют дельту для приблизительной оценки вероятности такого события. Например, если дельта опциона вне денег (OTM) равна 0,15, то вероятность выхода этого опциона в деньги и экспирации там приблизительно составляет 15%. Опционы около денег (ATM) имеют дельту около 0,5, что примерно соответствует 50% вероятности того, что они будут в деньгах на момент экспирации. Для более точного расчёта вероятности экспирации опциона в деньгах используется Dual Delta, которая является первой производной цены опциона по страйку.
Для двух европейских опционов call и put с общим базовым активом, ценой исполнения (страйком), датой экспирации и без дивидендных выплат, сумма абсолютных значений их дельт равна 1, другими словами, дельта call-опциона (положительна) минус дельта put-опциона (отрицательна) равно 1.
[b]Vega[/b]
Vega отражает чувствительность к изменению волатильности. Вега является производной цены опциона по отношению к волатильности базового актива.
[attachment=43]vega_f1.png[/attachment]
Для обозначения веги используется греческая буква ню ([attachment=50]nu.png[/attachment]). Учёные иногда обозначают вегу буквой каппа ([attachment=53]kappa.png[/attachment]), а также буквой тау ([attachment=46]tau.png[/attachment]), но значительно реже.
Вега обычно отражает количество денег, на которое увеличится (или уменьшится) стоимость опциона при увеличении (или снижении) волатильности базового актива на 1%. Если вега отрицательна, то стоимость опциона падает с ростом волатильности и растёт при снижении волатильности.
[b]Theta[/b]
Theta [attachment=45]theta.png[/attachment] отражает изменение стоимости опциона с течением времени, то есть величину временного распада.
[attachment=44]theta_f1.png[/attachment]
Математический результат, полученный по приведенной выше формуле, даёт значение в расчёте на год. Как правило, этот результат делят на количество дней в году, чтобы получить сумму денег, на которую снижается цена опциона за один день. Тета почти всегда отрицательна для купленных опционов и положительна для проданных. Исключением может являться европейский put-опцион, находящийся глубоко в деньгах (ITM). Величина теты для портфеля может быть определена как сумма тет для каждой отдельной позиции, входящей в портфель.
Стоимость опциона можно разделить на две части: внутреннюю стоимость и временн[i]у[/i]ю стоимость. Внутренняя представляет собой сумму денег, которую можно было бы получить, если исполнить опцион немедленно. То есть у call-опциона со страйком $50 при цене базового актива $60 внутренняя стоимость равна $10, при этом put-опцион того же страйка будет иметь нулевую внутреннюю стоимость. Оставшаяся часть цены опциона приходится на временную стоимость. Чем больше времени до экспирации, тем выше временная стоимость опциона (при прочих равных условиях) и медленнее временной распад. С приближением даты экспирации временной распад ускоряется (тета увеличивается по модулю), а временная стоимость уменьшается вплоть до нуля.
[b]Rho[/b]
Rho [attachment=48]rho.png[/attachment] является мерой чувствительности к величине безрисковой процентной ставки. Rho — это производная стоимости опциона по отношению к безрисковой процентной ставке.
[attachment=47]rho_f1.png[/attachment]
Rho обычно выражается в виде суммы денег, на которую увеличится (или уменьшится) цена опциона при повышении (или снижении) безрисковой процентной ставки на 1,0% годовых (100 базисных пунктов).
За исключением чрезвычайных обстоятельств, стоимость опциона менее чувствительна к изменениям безрисковой процентной ставки, чем к изменениям других параметров. По этой причине ро является наименее часто используемым греком первого порядка.
[b]Lambda[/b]
Lambda [attachment=52]lambda.png[/attachment], Omega [attachment=49]omega.png[/attachment] или упругость — величина, показывающая на сколько процентов изменится цена опциона при изменении цены базового актива на 1%. Её также называют рычагом, плечом, передачей.
[attachment=51]lambda_f1.png[/attachment]
Например, если цена опциона равна $5, дельта 0,2 и цена базового актива $100, то Lambda = 0,2 * $100/$5 = 4, то есть при увеличении цены базового актива на 1% ($1 от $100) цена опциона увеличится на 4% ($0,2).
[/spoiler]
[spoiler="Греки второго порядка"]
[size=120][b]Греки второго порядка[/b][/size]
[b]Gamma[/b]
Gamma [attachment=55]gamma.png[/attachment] показывает отношение скорости изменения дельты опциона к скорости изменения цены базового актива. Гамма является второй производной цены [attachment=59]V.png[/attachment] опциона по отношению к цене базового актива [attachment=58]S.png[/attachment]. Все купленные опционы имеют положительную гамму, все проданные — отрицательную. Наибольшее абсолютное значение гаммы имеют опционы около денег (ATM), которое постепенно уменьшается когда опцион становится в деньгах (ITM) или вне денег (OTM).
[attachment=54]gamma_f1.png[/attachment]
Когда трейдер стремится создать эффективный дельта-хеджированный портфель, он может также нейтрализовать гамму портфеля, что будет гарантировать эффективное хеджирование в более широком диапазоне ценовых движений базового актива. Однако, при нейтрализации гаммы портфеля, снижается коэффициент [url=http://calvera.ru/forum/viewtopic.php?f=33&t=143]альфа[/url].
[b]Vanna[/b]
Vanna, также известная как DdeltaDvol и DvegaDspot, является производной второго порядка от цены опциона по отношению к цене базового актива и волатильности. Математически она эквивалентна DdeltaDvol (первой производной дельты по волатильности), которая показывает чувствительность дельты опциона к изменению волатильности; или DvegaDspot (первой производной веги по цене базового актива), оценивающей изменение чувствительности опциона к изменению волатильности при движении цены базового актива. Vanna может быть полезна для контроля чувствительности дельта- или вега-хеджированного портфеля к изменению, соответственно, волатильности или цены базового актива.
[attachment=41]vanna_f1.png[/attachment]
[b]Vomma[/b]
Vomma, Volga, выпуклость веги, гамма веги или dTau/dVol — величина, отражающая чувствительность второго порядка к волатильности. Vomma является второй производной стоимости опциона по волатильности, или, другими словами, vomma измеряет скорость изменения веги при изменении волатильности. При положительной vomma, позиция становится более длинной по веге при увеличении подразумеваемой волатильности, и более короткой по веге при снижении IV.
[attachment=40]vomma_f1.png[/attachment]
[b]Charm[/b]
Charm или распад дельты отражает мгновенную скорость изменения дельты с течением времени. Charm также называют DdeltaDtime (первая производная дельты по времени). Charm является производной второго порядка от стоимости опциона по отношению к цене базового актива и времени. Это также производная теты по отношению к цене базового актива. Charm помогает поддерживать эффективный дельта-хедж, особенно при переносе позиции через выходные и праздники.
[attachment=39]charm_f1.png[/attachment]
Математический результат, полученный по вышеуказанной формуле, даёт значение в расчёте на год. Часто бывает полезно разделить его на количество дней в году, чтобы получить величину распада дельты за сутки. Такая оценка является достаточно точной, если количество дней до экспирации опциона относительно велико. При приближении даты экспирации charm может меняться довольно быстро, что заметно искажает суточную оценку распада дельты.
[b]Veta[/b]
Veta или DvegaDtime показывает скорость изменения веги с течением времени, или скорость распада веги. Veta — вторая производная цены опциона: по волатильности и по времени.
[attachment=38]veta_f1.png[/attachment]
Обычной практикой является деление результата, полученного по вышеуказанной формуле, на количество дней в году и на 100, чтобы получить процентное изменение веги за один день.
[b]Vera[/b]
Vera (иногда Rhova) показывает скорость изменения Rho при изменении волатильности. Вера является второй производной цены опциона: по волатильности и по безрисковой процентной ставке. Vera может быть использована для оценки воздействия изменения волатильности на Rho-хеджирование.
[attachment=37]vera_f1.png[/attachment]
[/spoiler]
[spoiler="Греки третьего порядка"]
[size=120][b]Греки третьего порядка[/b][/size]
[b]Color[/b]
Color, распад гаммы или DgammaDtime показывает скорость изменения гаммы с течением времени. Color — производная третьего порядка цены опциона: дважды по цене базового актива и один раз по времени. Color может быть полезен для прогнозирования изменения гамма-хеджа с течением времени.
[attachment=36]color_f1.png[/attachment]
Математический результат, полученный по вышеуказанной формуле, даёт значение в расчёте на год. Часто бывает полезно разделить его на количество дней в году, чтобы получить величину распада гаммы за сутки. Такая оценка является достаточно точной, если количество дней до экспирации опциона относительно велико. При приближении даты экспирации color может меняться довольно быстро, что заметно искажает суточную оценку распада гаммы.
[b]Speed[/b]
Speed показывает скорость изменения гаммы при изменении цены базового актива. Эту величину иногда называют гаммой гаммы или DgammaDspot. Speed — третья производная цены [attachment=59]V.png[/attachment] опциона по отношению к цене базового актива [attachment=58]S.png[/attachment]. Speed может быть полезна при мониторинге дельта- или гамма-хеджа портфеля.
[attachment=35]speed_f1.png[/attachment]
[b]Ultima[/b]
Ultima или DvommaDvol показывает чувствительность vomma к изменению волатильности. Ultima — третья производная стоимости опциона по волатильности.
[attachment=34]ultima_f1.png[/attachment]
[b]Zomma[/b]
Zomma или DgammaDvol показывает скорость изменения гаммы при изменении волатильности. Zomma — третья производная стоимости опциона: дважды по цене базового актива и один раз по волатильности. Zomma может быть полезна для мониторинга гамма-хеджа портфеля, и поможет трейдеру предвидеть изменения в эффективности хеджирования при изменении волатильности.
[attachment=33]zomma_f1.png[/attachment]
[/spoiler]
[spoiler="Формулы расчёта опционных греков"]
[size=120][b]Формулы расчёта греков[/b][/size]
Греки стандартных ([url=http://calvera.ru/forum/viewtopic.php?f=33&t=225]ванильных[/url]) опционов в рамках [url=http://calvera.ru/forum/viewtopic.php?f=33&t=224]модели Блэка-Шоулза[/url] для заданной цены базового актива [attachment=58]S.png[/attachment], цены исполнения опциона (страйке) [attachment=32]K.png[/attachment], безрисковой процентной ставке [attachment=31]r.png[/attachment], годовой дивидендной доходности [attachment=30]q.png[/attachment], времени до экспирации [attachment=29]tau_f1.png[/attachment] и волатильности [attachment=28]sigma.png[/attachment] рассчитываются следующим образом:
[table][tr][th][/th][th]Call-опционы[/th][th]Put-опционы[/th][/tr]
[tr][th]Цена опциона[/th][td][attachment=25]price_call.png[/attachment][/td][td][attachment=24]price_put.png[/attachment][/td][/tr]
[tr][th_colspan=3][/th_colspan][/tr]
[tr][th]Delta[/th][td][attachment=23]delta_call.png[/attachment][/td][td][attachment=22]delta_put.png[/attachment][/td][/tr]
[tr][th]Vega[/th][td_colspan=2][attachment=21]vega_call_put.png[/attachment][/td_colspan][/tr]
[tr][th]Theta[/th][td][attachment=20]theta_call.png[/attachment][/td][td][attachment=19]theta_put.png[/attachment][/td][/tr]
[tr][th]Rho[/th][td][attachment=18]rho_call.png[/attachment][/td][td][attachment=17]rho_put.png[/attachment][/td][/tr]
[tr][th_colspan=3][/th_colspan][/tr]
[tr][th]Gamma[/th][td_colspan=2][attachment=16]gamma_call_put.png[/attachment][/td_colspan][/tr]
[tr][th]Vanna[/th][td_colspan=2][attachment=15]vanna_call_put.png[/attachment][/td_colspan][/tr]
[tr][th]Charm[/th][td][attachment=14]charm_call.png[/attachment][/td][td][attachment=13]charm_put.png[/attachment][/td][/tr]
[tr][th_colspan=3][/th_colspan][/tr]
[tr][th]Speed[/th][td_colspan=2][attachment=12]speed_call_put.png[/attachment][/td_colspan][/tr]
[tr][th]Zomma[/th][td_colspan=2][attachment=11]zomma_call_put.png[/attachment][/td_colspan][/tr]
[tr][th]Color[/th][td_colspan=2][attachment=10]color_call_put.png[/attachment][/td_colspan][/tr]
[tr][th_colspan=3][/th_colspan][/tr]
[tr][th]Veta[/th][td_colspan=2][attachment=9]veta_call_put.png[/attachment][/td_colspan][/tr]
[tr][th]Vomma[/th][td_colspan=2][attachment=8]vomma_call_put.png[/attachment][/td_colspan][/tr]
[tr][th]Ultima[/th][td_colspan=2][attachment=7]ultima_call_put.png[/attachment][/td_colspan][/tr]
[tr][th_colspan=3][/th_colspan][/tr]
[tr][th]Dual Delta[/th][td][attachment=6]dualdelta_call.png[/attachment][/td][td][attachment=5]dualdelta_put.png[/attachment][/td][/tr]
[tr][th]Dual Gamma[/th][td_colspan=2][attachment=4]dualgamma_call_put.png[/attachment][/td_colspan][/tr][/table]
где
[attachment=3]d1.png[/attachment]
[attachment=2]d2.png[/attachment]
[attachment=27]phi_small.png[/attachment] — функция стандартной нормальной плотности вероятности
[attachment=1]phi_small_f1.png[/attachment]
[attachment=26]phi_big.png[/attachment] — функция стандартного нормального распределения
[attachment=0]phi_big_f1.png[/attachment]
[/spoiler]